Some of you might be wondering why a rectangle has diagonals that are the same length.

🦗🦗🦗

What, no one?

Why do we need to learn something new?

BECAUSE I TOLD YOU SO!

Wait, that belongs in the “Things I Learned From My Mother” post.

Um, it is up to you. If your brain starts hurting or you get a nose bleed, you might want to take a break or skip this one.

This article is about geometry and trigonometry. It spawned from the article about building a picnic table/bench. John was curious whether he could still solve the parallelogram geometry problem. Those two math classes were not his most successful ones.

Why are you being tortured with this? Because misery loves company!

These are some Geometry facts that will help with the article. From John’s education, angles get Greek letters (e.g., Φ, φ, σ) and lengths get capital English letters (e.g,, A, B, C)

• The inside angles of a triangle always add up to 180 degrees.
• The length of the hypotenuse (C) of a right triangle (one angle is 90 degrees) is the square root of the sum of the squares of the other two sides (A & B). This is the Pythagoras Theorem.

You can visualize it like this:

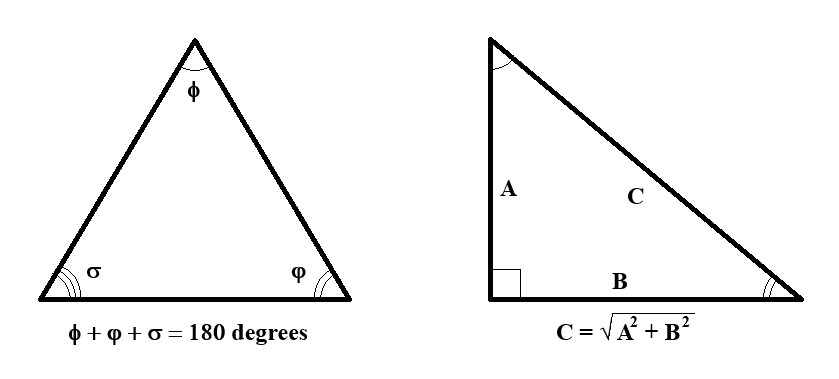
The arcs in the corners indicate same angles for same number of arcs. The square in the corner means the angle is 90 degrees.

Next, you need to understand some basic Trigonometry, such as sine and cosine.

No, those are both sign and co-sign. Sine and cosine are mathematical functions that give you the coordinates of points on a circles or the sides of a right triangle. The things to remember here are that:

• Sine is the fraction of the opposite side over the hypotenuse
• Cosine is the fraction of the adjacent side over the hypotenuse
• Sine squared plus cosine squared is always equal to one (for the same angle)
• A circle has 360 degrees, so sine and cosine repeat values after 360 degrees

Wut? I know, right. And impressionable children are forced to learn this. As a parent, you should be ashamed of yourself for not putting a stop to this.

Visualize it like this:

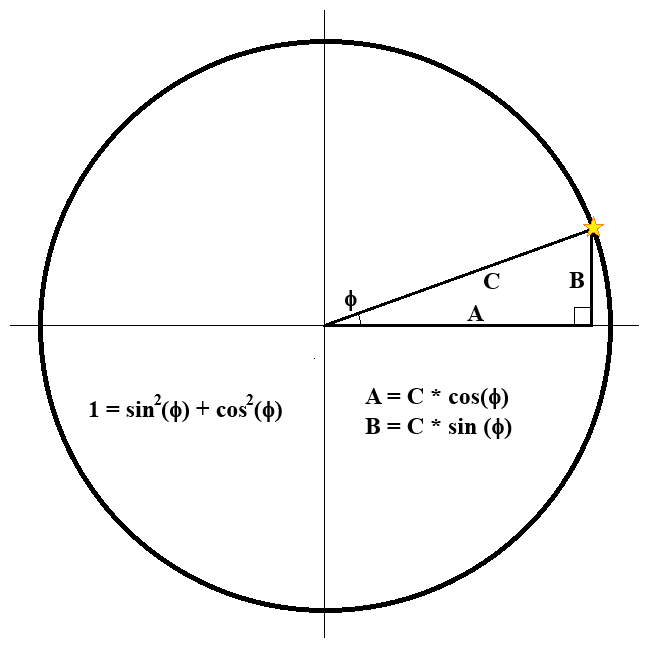
As you move the star around the edge of the circle, you can calculate the length of A and B, if you know the radius, C, and angle, Φ.

Huh…

Neat, right? Not useful for balancing your checkbook, but it is useful for building a picnic table.

There are a few other items, such as how to tell which angles are equal, but we will breeze over that and just mark them on the diagrams.

This is our parallelogram.

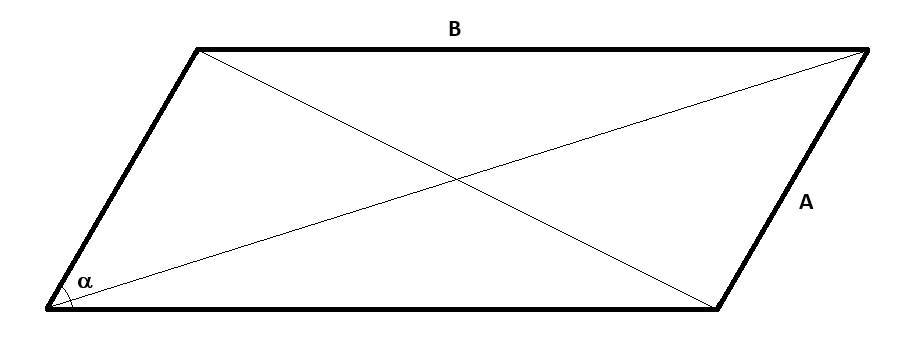
It is the epitome of evil, if you are trying to build something with square corners.

First, we will math the daylights out of the short diagonal. We can drop a (dotted) line from the upper left corner to the base to make a right angle to the top and bottom sides. We know that we can do this because, by the definition of a parallelogram, the opposite sides are parallel.

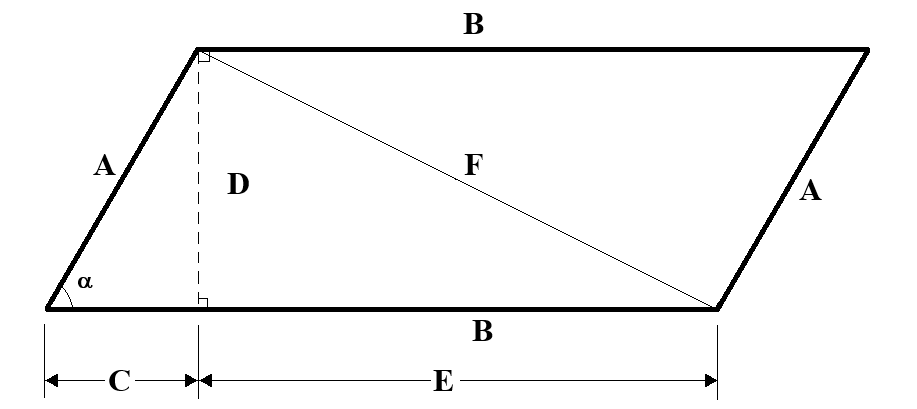
We can apply the rules above to calculate C and D from A and α. C and B can be used to calculate E. Finally, D and E can be used to calculate the diagonal, F.

C = A * cos(α)

D = A * sin(α)

E = B – C

Does it pass the sniff test? Woah! Math smells terrible. Despite that, it passes.

Why?

I am glad you asked. If this was a rectangle with 90 degree angles, the diagonal, F, would be √(A² + B²). The value that we calculated is shorter by a value that depends on the length of the sides and the angle. That is a believable answer. It could still be wrong, but it passes the sniff test.

Wow, math needs some deodorant.

You are not wrong.

The long diagonal works similar, but we have to extend the A side. The calculations follow the same general pattern as the ones above. The matching diagram is:

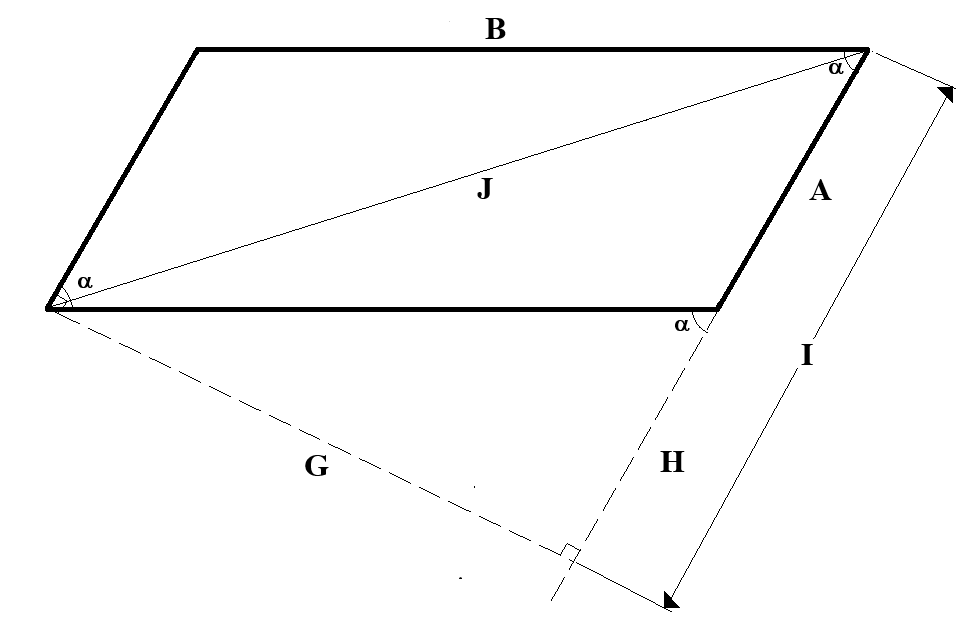
Similar to the equations above:

G = B * sin(α)

H = B * cos(α)

I = H + A

This passes the sniff test in the same way as the first result. The longer diagonal is longer by a length related to the two sides and the angle. The similarity in equations for the diagonals suggests that we are right or made the same mistake.

Our two diagonals are:

F = √[A² – 2 * A * B * cos(α) + B²]

J = √[A² + 2 * A * B * cos(α) + B²]

The real test is what happens when you plug in 90 degrees for α? If you look at the circle above, 90 degrees happens when the star is at the top of the circle. The cos(α) corresponds to the value of A on a circle with radius (i.e., C) of one. When the star is straight up, the horizontal distance, A, will have a length of zero. Zero multiplied by any number is zero, so when we plug in zero for cos(α), we get:

F = √[A² – 2 * A * B * 0 + B²] = √[A² + B²]

J = √[A² + 2 * A * B * 0 + B²] = √[A² + B²]

With 90 degree corners, the diagonals, F and J, are equal length.

This is the reason that measuring the diagonals works to verify a rectangle has 90 degree corners. There are caveats to this.

• The intended shape must be a rectangle. The opposite sides must be equal length. (A square is also a rectangle.)
• The sides must be stiff. Flexible sides may not stay straight enough to measure accurately.
• The sides have to be relatively flat, such as good quality 2″x4″ boards. If the boards are “U-shaped”, this will not necessarily work.

Was that as painful as you expected?

Yes!

La-la-la, I am not listening!